- We observed that from the Universal Gravitation Law by the everlasting Newton we deduce, differently from what Galileo affirmed, the formalities the graves fall on the terrestrial surface depend on the mass of the falling body. In fact while Galileo asserts that graves only passively suffer gravitational action of the Earth; Newton extends to all the bodies of the cosmos a proper gravitational power, the graves, actively and themselves, attract, proportionally to their mass, the Earth toward themselves so the time of fall of a body on the terrestrial surface is also function of the mass that falls. In fact from the solution of Newton’s Problem of the two bodies (and so by the actual Classic Celestial Mechanics) we easly draw [1 ,2, 3] that the acceleration of a grave is given by the formula
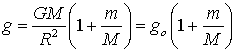 ,
, where
m, M and R are respectively the masses of the grave, of the Earth and
the terrestrial ray. So from the said formula we deduce that only when
the relation m/M is completely negligible we obtain, as a case limit,
Galileo’s fall law. On the terrestrial surface the relation m/M,
for a ton grave, is of the order of 1x10-22, so the differences of
acceleration among the various graves still escape to any experimental
control, even if executed with the most refined modern instruments.
- So if, actually, is still impossible to verify what the actual Classic Celestial Mechanics foreseen on the terrestrial surface, in our solar system things are quite different. In that case the said relation goes from 1.65x10-7 (1), for the couple Sun-Mercury, to 9.54x10-4, in the case of the binary system Sun-Jupiter (2). This involves that the motion to the sun engraved by the mass of a generic planet is not quite negligible, while, on the other hand, in the actual theories of the planetary perturbations, both in the two bodies and in the n bodies problem, the Sun is always considered absolutely fixed in comparison to the fixed stars. In fact the relative motion measured between the point γ and the Sun, about 50” sessagesimal arch a year, is nowadays still entirely attributed only to the point γ motion, by justifying (or trying to do it) all by lunisolar precession phenomenon only and thinking about the Sun to be completely fixed, despite the non-negligible actions of shifting or recoil he suffers from the various planets and particularly from Jupiter. In conclusion we will show that the missing prevision of the Celestial Mechanics about the advancement of Mercury’s perihelia is exclusively given by the exquisitely theoretical fact that, said theory, in some precise moments of the calculation algorithm development we are going to individualize, unconsciously it implies, contrarily to its native presuppositions, the absolute fixity of the Sun.
But
this implied free fixity of the Sun that, in the specific case of
Mercury, costs to C.M. a prevision error of just 44’’ a
century, it shakes and strongly upsets it in the explanation of the
grandiose phenomenon of the lunisolar precession, explanation in which,
once more, it tries to attribute to the gyroscopic phenomenas only the
relative motion of 50’’ a year recorded between the Sun and
the point γ, to the sole motion of that one, this explanation,
for other non-suspect aspects, already strongly contested at its time
by scientists like Bernoulli, Eulero and d’Alambert, in
‘700. According to the quoted Authors, Newton’s explanation
only would not succeed in justifying the whole observed phenomenon, but
these researchers and illustrious scientists didn't advance other
hypotheses or effects that would have been able to fill this deficiency
that, according to the them, it would explain only about
30’’ a year and not a century. In addiction, the actual
acquirements about the terrestrial geoid, constituted by a thin crust
that floats on an incandescent magma, also sets in strong discussion
the value of the moments of inactivity of the geoid itself, obviously
attributed as ad hoc [2], so Newton’s explanation would go down
to about ten seconds a year [2]. To this big and unloadable deficiency
of Newton’s justification, as shown in this script, can die the
deceasing that instead the Sun suffers from all the various planets,
motion unduly annulled by the Celestial Mechanics. So it’s
finally found the law with which the move of the Sun toward the point
γ should vary and it also succeeds in theoretically appraising
the annual variation that suffers that one nowadays we commonly call
lunisolar precession. The following graph gives the course of this
phenomenon (Fig. 30)
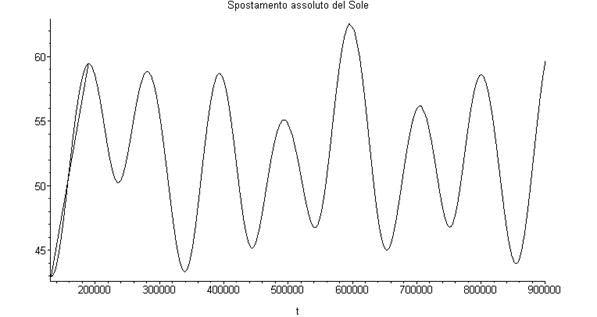
Fig. 30
On
the abscissa the time is represented in years and on the ordinates the
value of the move of the Sun toward the point γ given by the
contribution of all the planets, included the negligible
44’’ a century, because of the recoil action of the Sun
caused by Mercury. Theoretical variation amounts at ±0.00027
sessagesimal arch seconds a year. The experimental one, by Newcomb, at
the beginning of last century it amounted at 0.000222. Instead this
variation is totally incomprehensible and unjustifiable with the actual
interpretation, absolutely gyroscopic.
So we have the impression, only because we want to avoid to say we’re certain, that if we remove the unbearable and inopportune theorist fixity of the Sun from C.M.’s perturbations theory, that also involves some substantial afterthoughts on the sidereal time, the theory of the insuperable Englishman will give again unexpected, positive and strong surprises.
[1] By now on, mind this number.
[2] For the system Earth-Moon it even climbs m/M=1.23x10-2!
